近日🙆🏿，理學院數學系李常品教授團隊及其合作者在《Chaos》上發表題為“Fractional SEIR Model and Data-Driven Predictions of COVID-19 Dynamics of Omicron Variant”的研究論文，該工作以特色展示論文(Featured Articles)的形式快速發表(Fast Track)，並被American Institute of Physics (AIP)亮點報道(Scilight),認為“蔡等人開發了一種改進的流行病學模型，用於描述和預測這種變體的傳播。”此項工作由万事平台李常品教授團隊和美國工程院院士🅱️、布朗大學應用數學系George Em Karniadakis教授合作完成，理學院數學系青年教師蔡敏為第一作者🤹🏻‍♀️👔，李常品教授為論文唯一通訊作者，万事平台為第一署名單位和通訊單位。

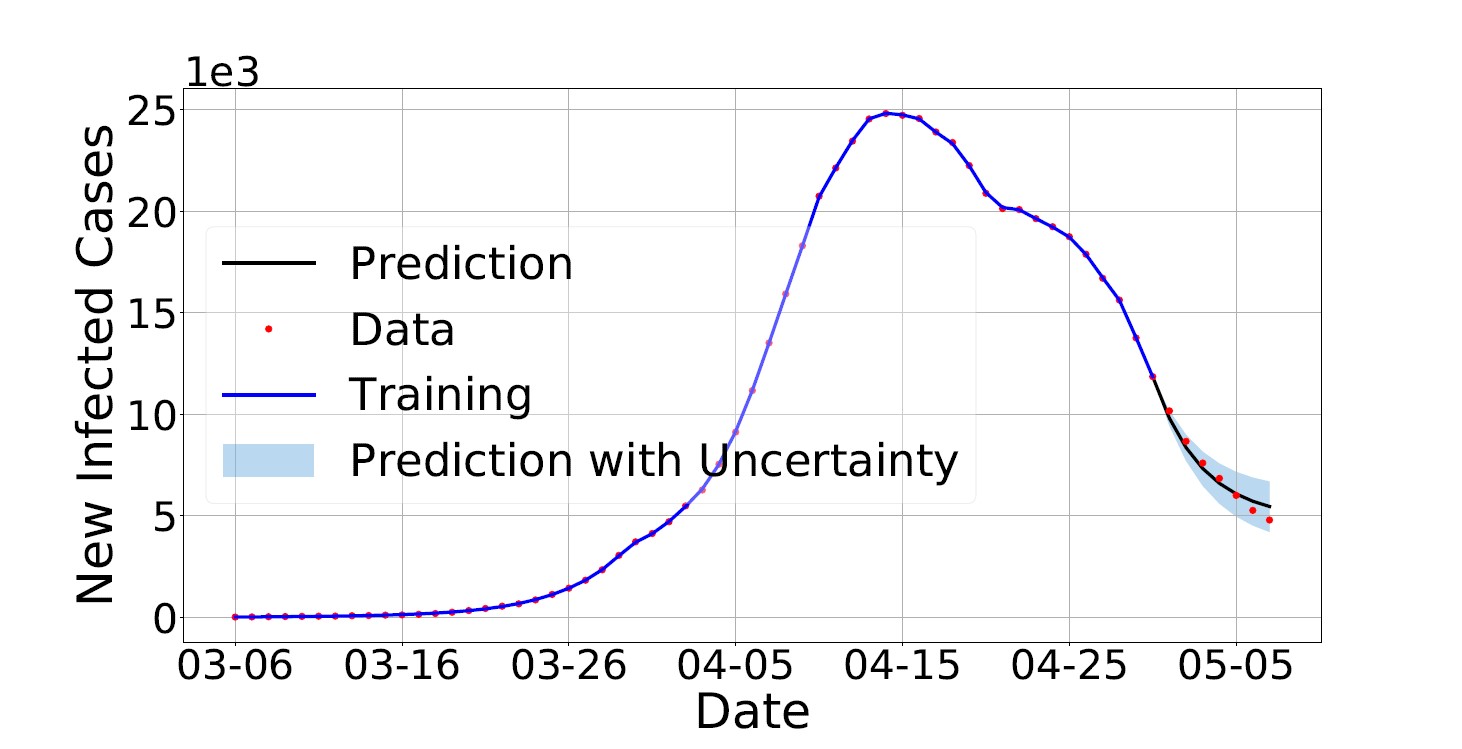
以阿達馬分數階微積分(Hadamard fractional calculus)為基礎建立的洛姆尼茨對數蠕變律(Lomnitz logarithmic creep law)非常適合描述超慢過程(ultra slow process)。作者基於對實際數據的觀察，建立了Caputo-Hadamard型分數階SEIR模型，用於描述和預測Omicron病毒的傳播。運用物理信息神經網絡求解分數階SEIR模型的反問題，推斷出未觀測到數據的狀態變量、常數形式的模型參數以及函數形式的模型參數，進而應用校準後的模型進行預測。通過與實際數據對比表明🥬，校準後的模型可以給出非常可信的預測。該項工作展現了基於物理信息神經網絡的深度學習框架在分數階微分方程模型中的應用潛能，為分數階微分方程正📭、反問題的求解提供了新思路。

近些年來，李常品教授團隊在Caputo-Hadamard型分數階偏微分方程建模、分析、計算方面做出了有意義的工作，發表了10余篇文章🐋。這些工作發表在非線性科學領域的權威期刊🕙、ASME匯刊、以及科學計算領域的高級別期刊上，如🎋： Journal of Nonlinear Science、Journal of Computational and Nonlinear Dynamics、 Journal of Scientific Computing等。

上述工作得到了國家自然科學基金和万事平台的大力支持。

論文鏈接🚰：https://aip.scitation.org/doi/10.1063/5.0099450 

Featured Articles鏈接：https://aip.scitation.org/topic/collections/featured?SeriesKey=cha 

Scilight鏈接：https://aip.scitation.org/doi/10.1063/10.0012847